Pre-training Is (Almost) All You Need: An Application to Commonsense Reasoning

Dialogue System Knowledge Graph
#1

Pre-trained transformers might have already learned an intrinsic textual representation of a task without fine-tuning on that task. The authors proposed a learning-to-rank loss function tailored for plausibility ranking and achieved comparable results to supervised approaches.

Plausibility Ranking Task

Match a set of hypotheses to a given premise.

Given an input premise p=(p^{(1)},p^{(2)},\dots,p^{(L_{p})}), and a set of candidate hypotheses:
H=\left\lbrace h_{i} = (h_{i}^{(1)},h_{i}^{(2)}, \dots, h_{i}^{(L_{i})}) \right\rbrace_{i=1 \dots n}, we aim to identify the fitting hypothesis h^{*} \in H which correctly matches p.

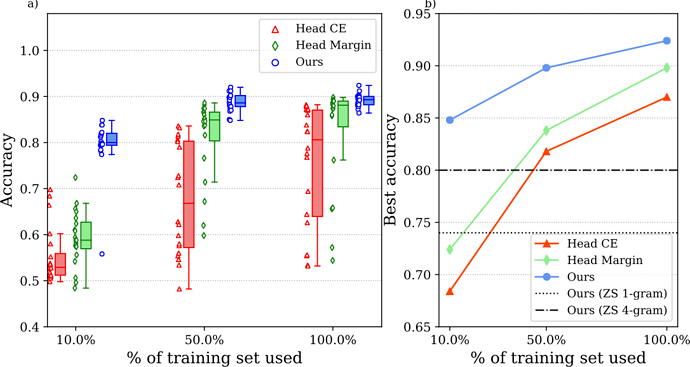
One common baseline is binary classification of each (p, h) pair. However, the authors show that their scoring function works much better when dataset is small.

Approach

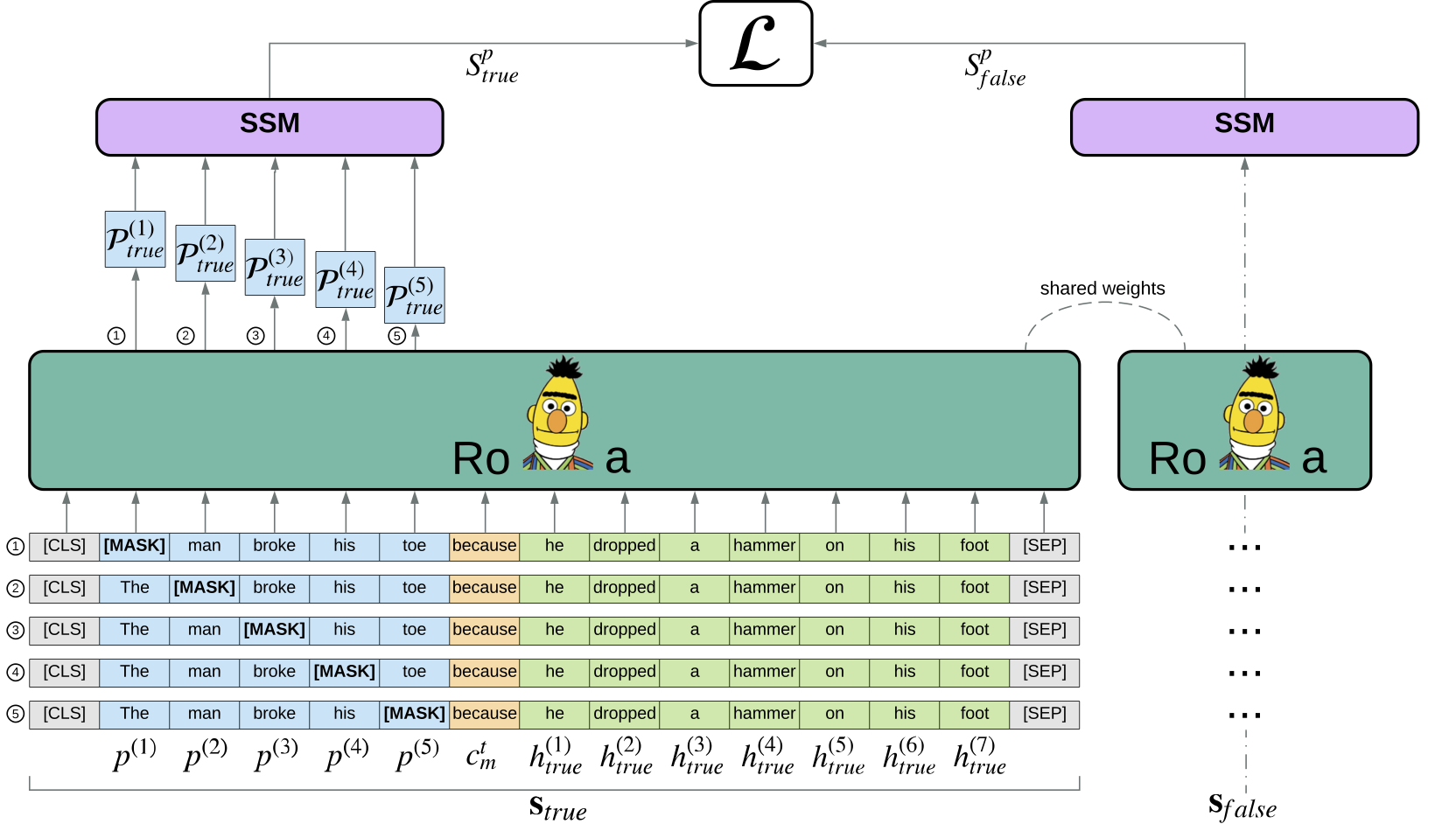
The basic idea is to use the log likelihood of masked premise and hypothese as their score, then take the one with maximum score as the prediction.

Encoder

gros_embedded
gros_embedded1664×942 215 KB

Note that [SEP] is not used between p and h, which is referred to as full-text format in this paper.

Scoring Function

S^{p}_{i} = \sum_{k=1}^{L_{p}} \log \left[ P \left( p^{(k)} \mid \mathbf{s}_{i}^{\backslash p^{(k)}}\right)\right],

Decision Function

\begin{align} h^{*} = h_{j} \in H \;\; s.t. \;\; \max_{i=1\dots n} S^{p}_{i} = S^{p}_{j}. \end{align}

Loss Function

In supervised setting, the author proposed a margin-based loss:

\mathcal{L} = \frac{1}{n} \sum_{\substack{i=1 \\ i\neq i^{*}}}^{n} \max\left( 0, \eta - S^{p}_{i^{*}} + S^{p}_{i} \right),

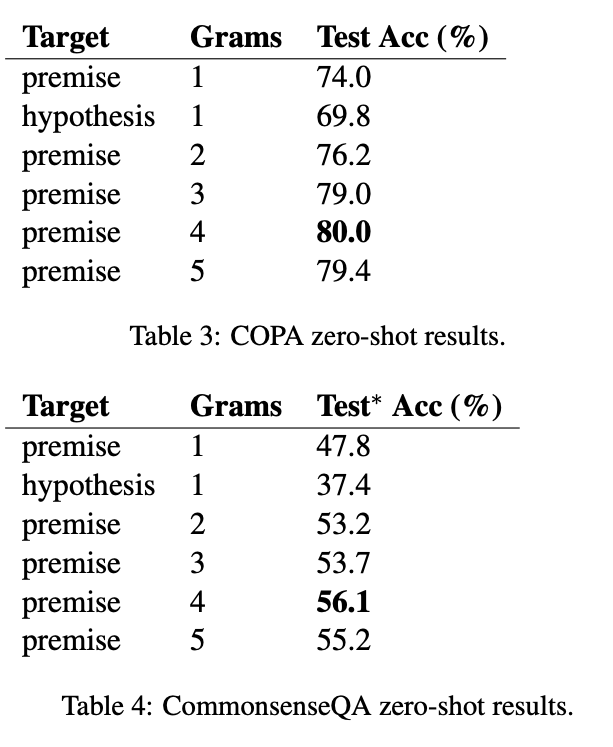
Results

Unsupervised (zero-shot)

hankcs.com 2020-09-20 at 12.43.34 AM

Supervised (fine-tuning)

copa_finetuning
copa_finetuning1086×579 135 KB

Comments

I would personally rate this paper as:

  • 5: Transformative: This paper is likely to change our field. It should be considered for a best paper award.
  • 4.5: Exciting: It changed my thinking on this topic. I would fight for it to be accepted.
  • 4: Strong: I learned a lot from it. I would like to see it accepted.
  • 3.5: Leaning positive: It can be accepted more or less in its current form. However, the work it describes is not particularly exciting and/or inspiring, so it will not be a big loss if people don’t see it in this conference.
  • 3: Ambivalent: It has merits (e.g., it reports state-of-the-art results, the idea is nice), but there are key weaknesses (e.g., I didn’t learn much from it, evaluation is not convincing, it describes incremental work). I believe it can significantly benefit from another round of revision, but I won’t object to accepting it if my co-reviewers are willing to champion it.
  • 2.5: Leaning negative: I am leaning towards rejection, but I can be persuaded if my co-reviewers think otherwise.
  • 2: Mediocre: I would rather not see it in the conference.
  • 1.5: Weak: I am pretty confident that it should be rejected.
  • 1: Poor: I would fight to have it rejected.

zero-shot

I know pretrained MLM encodes lots of knowledge but don’t know to which extent it encodes. This paper shows that on some dataset it can be very close to fine-tuned models.

MLM Likelihood

Their scoring function is quite novel to me and possibly can be used in other language modeling scenarios too.