SMART: Robust and Efficient Fine-Tuning for Pre-trained Natural Language...

Language Model
#1

To prevent pretrained transformers from overfitting and aggressive updating, this paper proposed two regularization methods.

Smoothness-Inducing Adversarial Regularization

The main idea is forcing the model to produce similar prediction for neighboring data points.

\begin{align} \textstyle\min_{\theta} \mathcal{F}(\theta)=\mathcal{L}(\theta) + \lambda_{\rm s} \mathcal{R}_{\rm s}(\theta), \end{align}

where \mathcal{L}(\theta) is the loss function defined as

\begin{align*} \textstyle\mathcal{L}(\theta) = \frac{1}{n}\sum_{i=1}^n\ell(f(x_i;\theta),y_i), \end{align*}

and \ell(\cdot,\cdot) is the loss function depending on the target task, \lambda_{\rm s}>0 is a tuning parameter, and \mathcal{R}_{\rm s}(\theta) is the smoothness-inducing adversarial regularizer. Here we define \mathcal{R}_{\rm s}(\theta) as

\begin{align*} \mathcal{R}_{\rm s}(\theta) = \frac{1}{n}\sum_{i=1}^n \max_{\|\tilde{x}_i-x_i\|_p \leq \epsilon} \ell_{\rm s}(f(\tilde{x}_i;\theta),f(x_i;\theta)), \end{align*}

\ell_{\rm s} is chosen as the symmetrized KL-divergence, i.e.,

\ell_{\rm s}(P,Q) = \mathcal{D}_{\rm KL}(P||Q)+ \mathcal{D}_{\rm KL}(Q||P);

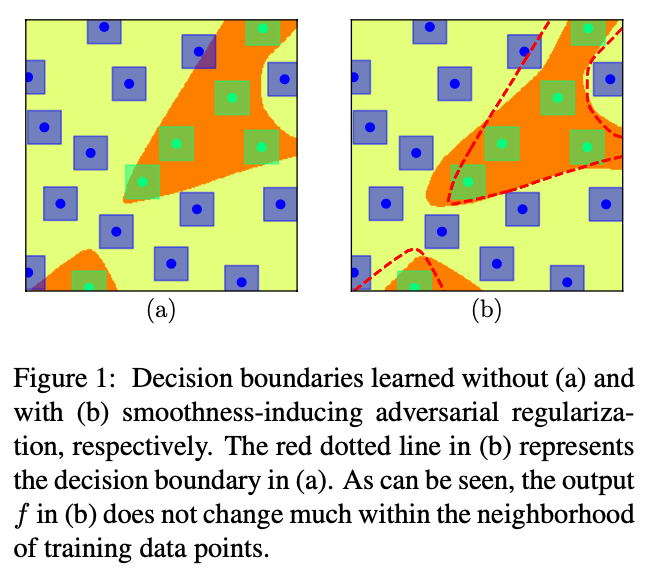
\tilde{x}_i is the generated neighbors of training points, serving as augmented data as shown in the following figure.

1

Bregman Proximal Point Optimization

It’s nothing else but a regularization term forcing the updation of parameters to be gentle.

\begin{align} \textstyle\theta_{t+1} = \mathop{\mathrm{argmin}}_{\theta}\mathcal{F}(\theta) + \mu\mathcal{D}_{\rm Breg}(\theta,\theta_t), \end{align}

where \mu>0 is a tuning parameter, and \mathcal{D}_{\rm Breg}(\cdot ,\cdot) is the Bregman divergence defined as

\begin{align*} \textstyle\mathcal{D}_{\rm Breg}(\theta,\theta_t) = \frac{1}{n}\sum_{i=1}^n \ell_{\rm s}(f(x_i;\theta), f(x_i;\theta_t)), \end{align*}

\ell_{\rm s} is the symmetrized KL-divergence mentioned above.

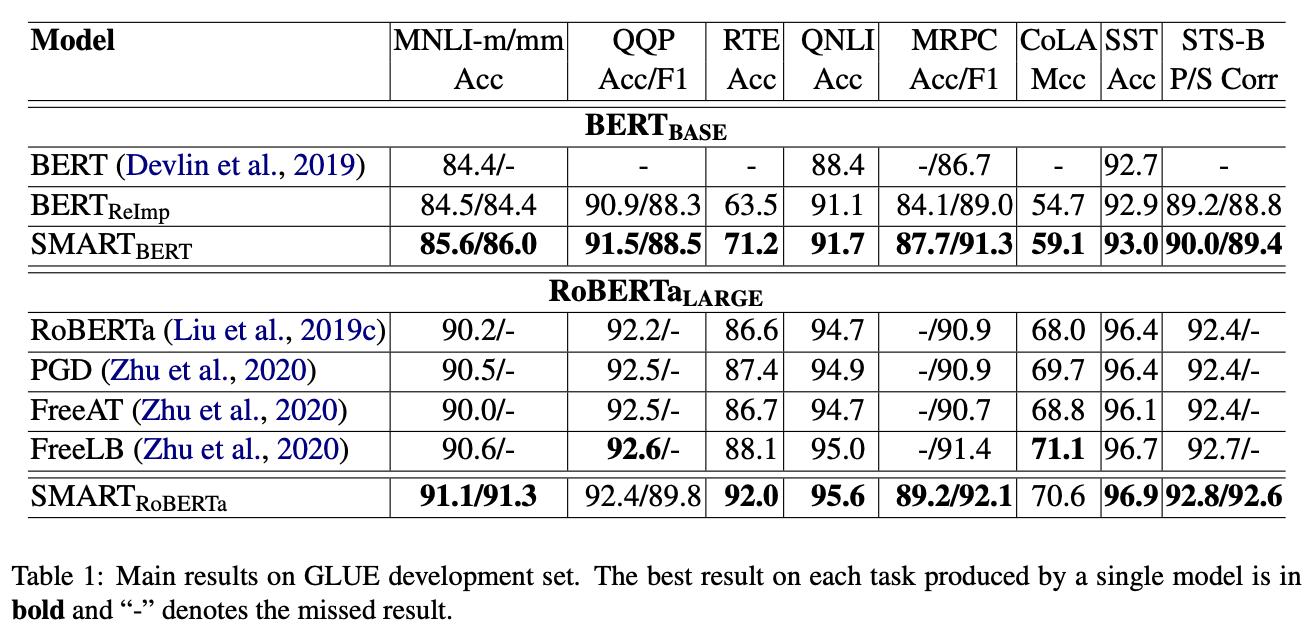
Results

res
res1314×632 178 KB

Their method consistently outperforms baseline.

Comments

This paper looks scary at the first glance as there seems to be a lot of equations. But it turns out to be easy to follow.

  • 5: Transformative: This paper is likely to change our field. It should be considered for a best paper award.
  • 4.5: Exciting: It changed my thinking on this topic. I would fight for it to be accepted.
  • 4: Strong: I learned a lot from it. I would like to see it accepted.
  • 3.5: Leaning positive: It can be accepted more or less in its current form. However, the work it describes is not particularly exciting and/or inspiring, so it will not be a big loss if people don’t see it in this conference.
  • 3: Ambivalent: It has merits (e.g., it reports state-of-the-art results, the idea is nice), but there are key weaknesses (e.g., I didn’t learn much from it, evaluation is not convincing, it describes incremental work). I believe it can significantly benefit from another round of revision, but I won’t object to accepting it if my co-reviewers are willing to champion it.
  • 2.5: Leaning negative: I am leaning towards rejection, but I can be persuaded if my co-reviewers think otherwise.
  • 2: Mediocre: I would rather not see it in the conference.
  • 1.5: Weak: I am pretty confident that it should be rejected.
  • 1: Poor: I would fight to have it rejected.