Graph Transformer for Graph-to-Sequence Learning

Linguistics Abstract Meaning Representation
#1

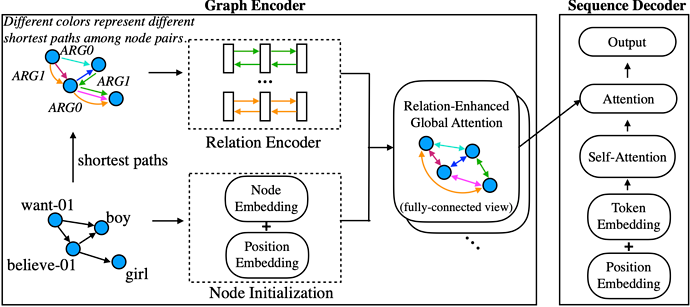
Early Graph NNs limit their message passing to first-order neighborhoods, while this paper enables global communication between two arbitrary nodes. Their proposed Graph Transformer shows a significant superiority over previous SOTA by a large margin.

Approach

arch
arch1784×796 235 KB

Graph Encoder

Relation Encoding

For a relation embedding r_{ij} between the node i and the node j, first split the relation encoding r_{ij} into the forward relation encoding r_{i\to j} and the backward relation encoding r_{j\to i}.

\begin{align} & [r_{i\to j}; r_{j\to i}] = W_r r_{ij} \end{align}

Then compute the attention score based on both the node representations and their relation representation:

\begin{align} \begin{split} s_{ij} &= g(x_i, x_j, r_{ij}) \\ & = (x_i + r_{i\to j})W_q^TW_k(x_j + r_{j\to i})\\ &= \underbrace{x_iW_q^TW_kx_j}_{(a)} + \underbrace{x_iW_q^TW_kr_{j\to i}}_{(b)} \\ &+ \underbrace{r_{i\to j}W_q^TW_kx_j}_{(c)} + \underbrace{r_{i\to j}W_q^TW_kr_{j\to i}}_{(d)} \end{split} \end{align}
  • a captures purely content-based addressing
  • b represents a source-dependent relation bias
  • c governs a target-dependent relation bias
  • d encodes the universal relation bias

A potential limitation of this split is that it still lacks some terms to model x_i, x_j and r_{i\to j} as a whole.

Multi-hop Encoding

Relation encoding can only encode the relation between neighbors. The authors extends it to multi-hop encoding using GRU over the sequence of relations:

Formally, they represent the shortest relation path sp_{i \to j} = [e(i, k_1), e(k_1, k_2), \ldots, e(k_n, j)] between the node i and the node j, where e(\cdot, \cdot) indicates the edge label and k_{1:n} are the relay nodes. They employ bi-directional GRUs for sequence encoding:

\begin{align*} \overrightarrow{s_t} &= \text{GRU}_f( \overrightarrow{s_{t-1}}, sp_t) \\ \overleftarrow{s_t} &= \text{GRU}_b(\overleftarrow{s_{t+1}}, sp_t) \end{align*}

The last hidden states of the forward GRU network and the backward GRU networks are concatenated to form the final relation encoding r_{ij} = [ \overrightarrow{s_n}; \overleftarrow{s_0}].

Patches

  • To facilitate communication in both directions, they add reverse edges to the graph

    • draw a virtual edge \texttt{believe-01}\stackrel{RARG1}{\longrightarrow}\texttt{want-01} according to the original edge \texttt{want-01}\stackrel{ARG1}{\longrightarrow}\texttt{believe-01}.

  • For convenience, they also introduce self-loop edges for each node.

    • With self-loop, every pair of nodes can be treated universally.

  • introduce an extra global node into every graph, who has a direct edge to all other nodes with the special label global. The final representation x_{global} of the global node serves as a whole graph representation.

Sequence Decoder

Their sequence decoder works similar to what people always use in sequential Transformer decoder:

  1. the global graph representation x_{global} is used to initialize the hidden states h_t at each time step
  2. h_t is then updated by interleaving multiple rounds of attention over the output of the encoder (node embeddings) and attention over previously-generated tokens (token embeddings)
  3. the final h_t is fed into softmax and copy mechanism for next token prediction:
    • \begin{align*} P(y|h_t) = P(gen|h_t) gen(y|h_t) +P(copy|h_t) \sum_{i \in S(y)} a_t^i \end{align*}

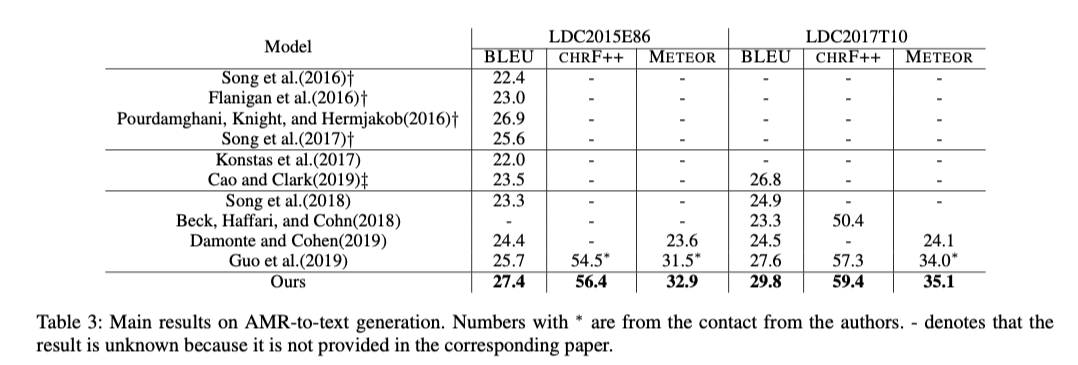
Experiments

1
11078×365 94.8 KB

Analysis

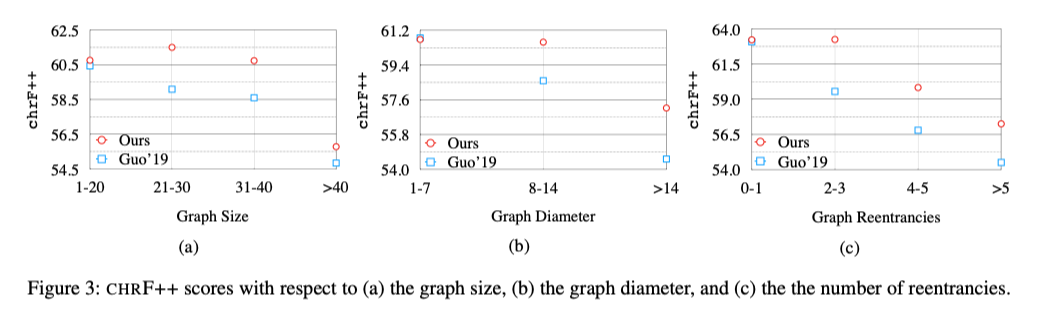
How does Graph Complexity affect performance

2
21037×309 67.8 KB

Seems that their model works better when the graph diameter is large.

How far are these heads attending to

3

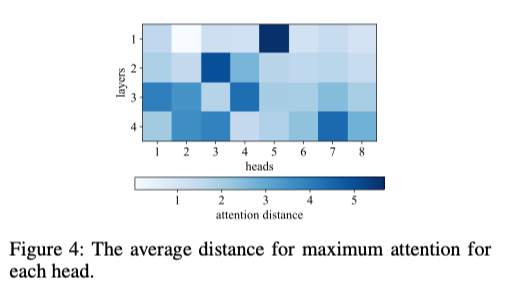
I don’t quite trust these attention heat maps, basically you get different heat maps every time you train a new model.

Comments

It’s not hard to come up with such ideas (using RNN for relation encoding), as there have been lots of paper encoding dependency relations along shortest path to the root. But I do admire their engineering efforts to make it work on Transformers.

  • 5: Transformative: This paper is likely to change our field. It should be considered for a best paper award.
  • 4.5: Exciting: It changed my thinking on this topic. I would fight for it to be accepted.
  • 4: Strong: I learned a lot from it. I would like to see it accepted.
  • 3.5: Leaning positive: It can be accepted more or less in its current form. However, the work it describes is not particularly exciting and/or inspiring, so it will not be a big loss if people don’t see it in this conference.
  • 3: Ambivalent: It has merits (e.g., it reports state-of-the-art results, the idea is nice), but there are key weaknesses (e.g., I didn’t learn much from it, evaluation is not convincing, it describes incremental work). I believe it can significantly benefit from another round of revision, but I won’t object to accepting it if my co-reviewers are willing to champion it.
  • 2.5: Leaning negative: I am leaning towards rejection, but I can be persuaded if my co-reviewers think otherwise.
  • 2: Mediocre: I would rather not see it in the conference.
  • 1.5: Weak: I am pretty confident that it should be rejected.
  • 1: Poor: I would fight to have it rejected.
1 Like