A Generative Model for Joint Natural Language Understanding and Generation

[1114]

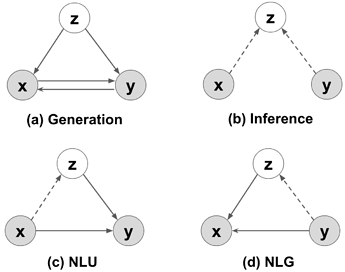
This paper proposes a novel joint framework for NLU and NLG using neural variational inference. Their method is capable of supervised, on-the-fly data augmentation and semi-supervised learning.

Following the standard variational inference, a latent variable z shared by the natural utterance x and the formal representation y is introduced.

As NLU is a many-to-one mapping problem, for NLU \mathbf{z} is sampled from a normal distribution

\begin{align} \label{eq:nlg-sample} \begin{split} & \pmb{\epsilon} \sim \mathcal{N}(0, \mathbf{I}) \\ & \mathbf{z} = \pmb{\mu}_{y,z} + \pmb{\sigma}_{y, z} \pmb{\epsilon} \end{split} \end{align}

where the mean and variance is learnt by some RNN models. NLG is instead a one-to-many problem so for NLG the mean vector \pmb{\mu}_{x,z} is used as \mathbf{z}.

Once \mathbf{z} is determined, it is concatenated with the decoder hidden states for NLU/NLG prediction.

For optimization, standard variational lower bound can be optimized for p(x,y) and p(x) or p(y). Depends on wether this x or y comes from auto-encoders or unlabelled data, the learning is called data-augmentation (marginal) or semi-supervised. In summary, the following optimizations are supported:

\begin{align} \mathcal{L}_{basic} &= \sum_{(x,y) \sim (X,Y) }( \mathcal{L}_{x, y} + \mathcal{L}_{y, x}) \\ \mathcal{L}_{marginal} &= \mathcal{L}_{basic} + \sum_{(x,y) \sim (X,Y) }(\mathcal{L}_{x} + \mathcal{L}_{y}) \\ \mathcal{L}_{semi} &= \mathcal{L}_{basic} + \sum_{x \sim X} \mathcal{L}_{x} + \sum_{y \sim Y} \mathcal{L}_{y} \end{align}

Comments

• Beautiful, what else can I say?
• I feel once graph encoder and decoder become matured, this method will bring us more benefits.

Rating

• 5: Transformative: This paper is likely to change our field. It should be considered for a best paper award.
• 4.5: Exciting: It changed my thinking on this topic. I would fight for it to be accepted.
• 4: Strong: I learned a lot from it. I would like to see it accepted.
• 3.5: Leaning positive: It can be accepted more or less in its current form. However, the work it describes is not particularly exciting and/or inspiring, so it will not be a big loss if people don’t see it in this conference.
• 3: Ambivalent: It has merits (e.g., it reports state-of-the-art results, the idea is nice), but there are key weaknesses (e.g., I didn’t learn much from it, evaluation is not convincing, it describes incremental work). I believe it can significantly benefit from another round of revision, but I won’t object to accepting it if my co-reviewers are willing to champion it.
• 2.5: Leaning negative: I am leaning towards rejection, but I can be persuaded if my co-reviewers think otherwise.
• 2: Mediocre: I would rather not see it in the conference.
• 1.5: Weak: I am pretty confident that it should be rejected.
• 1: Poor: I would fight to have it rejected.

A Generative Model for Joint Natural Language Understanding and Generation