SPARTA: Efficient Open-Domain Question Answering via Sparse Transformer...

Dialogue System
#1

This paper presents a practical method to enable large scale open-domain QA through pre-computed sparse index which can be implemented using Lucene.

They formulate document based QA as follows:

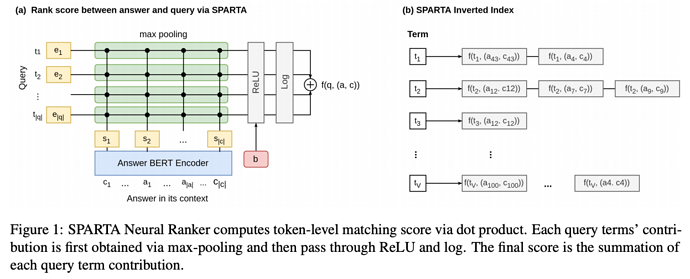
Let q be the input question, and A=\{(a, c)\} be a set of candidate answers. Each candidate answer is a tuple (a, c) where a is the answer text and c is context information about a. The objective is to find model parameter \theta that rank the correct answer as high as possible, .i.e:

\newcommand{\argmin}{\mathop{\mathrm{argmin}}\limits} \newcommand{\argmax}{\mathop{\mathrm{argmax}}\limits} \DeclareMathOperator{\EX}{\mathbb{E}}% expected value \begin{equation} \theta = \argmax_{\theta \in \Theta} \EX[p_{\theta}((a^*, c^*)|q)] \end{equation}

Then they embed query and answer separately using non-contextualized and contextualized embeddings.

\begin{align} \mathcal{E}(q) = [e_1, ... e_{|q|}] \quad \text{Query Embedding}&\\ \mathcal{H}(a, c) = [s_1, ... s_{|c|}] \quad \text{Answer Embedding}& \end{align}

Then dot product followed by max-pooling and ReLU is used to compute the matching score.

\begin{align} y_i = \text{max}_{j \in [1, |c|]} (e_i^T s_j) \quad \text{Term Matching}& \label{eq:term_match}\\ \phi(y_i) = \text{ReLU}(y_i + b) \quad \text{Sparse Feature}& \label{eq:sparse}\\ f(q, (a, c)) = \sum_{i=0}^{|q|}\log(\phi(y_i)+1) \quad \text{Final Score}& \end{align}

As query embeddings are independent to each other, their relevance to each candidate answer can pre-computed, which allows Lucene to index them.

1
11247×506 181 KB

Comments

  • It’s hard to believe that such a simple method performed so well. But if it’s true then this is a good paper.
Rating
  • 5: Transformative: This paper is likely to change our field. It should be considered for a best paper award.
  • 4.5: Exciting: It changed my thinking on this topic. I would fight for it to be accepted.
  • 4: Strong: I learned a lot from it. I would like to see it accepted.
  • 3.5: Leaning positive: It can be accepted more or less in its current form. However, the work it describes is not particularly exciting and/or inspiring, so it will not be a big loss if people don’t see it in this conference.
  • 3: Ambivalent: It has merits (e.g., it reports state-of-the-art results, the idea is nice), but there are key weaknesses (e.g., I didn’t learn much from it, evaluation is not convincing, it describes incremental work). I believe it can significantly benefit from another round of revision, but I won’t object to accepting it if my co-reviewers are willing to champion it.
  • 2.5: Leaning negative: I am leaning towards rejection, but I can be persuaded if my co-reviewers think otherwise.
  • 2: Mediocre: I would rather not see it in the conference.
  • 1.5: Weak: I am pretty confident that it should be rejected.
  • 1: Poor: I would fight to have it rejected.

0 投票者