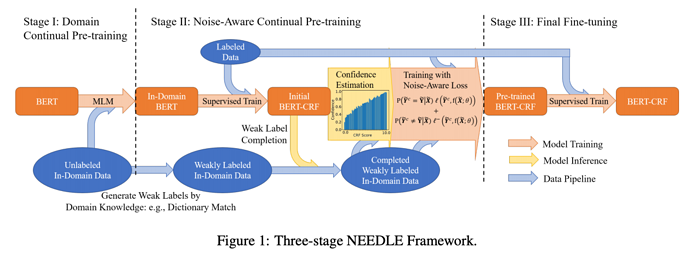
This paper fine-grained weakly supervised data to high and low confident ones and design a noise-aware loss function to learn them. They first train a supervised tagger to predict silver data. Then they correct the silver data with some domain knowledge. These corrected data is grouped into high and low confident categories which are learnt aggressively and conservatively. Accordingly, the noise-aware loss function is designed as
\newcommand{\bm}[1]{\boldsymbol{#1}}
\newcommand{\bA}{\bm{A}}
\newcommand{\bB}{\bm{B}}
\newcommand{\bC}{\bm{C}}
\newcommand{\bD}{\bm{D}}
\newcommand{\bE}{\bm{E}}
\newcommand{\bF}{\bm{F}}
\newcommand{\bG}{\bm{G}}
\newcommand{\bH}{\bm{H}}
\newcommand{\bI}{\bm{I}}
\newcommand{\bJ}{\bm{J}}
\newcommand{\bK}{\bm{K}}
\newcommand{\bL}{\bm{L}}
\newcommand{\bM}{\bm{M}}
\newcommand{\bN}{\bm{N}}
\newcommand{\bO}{\bm{O}}
\newcommand{\bP}{\bm{P}}
\newcommand{\bQ}{\bm{Q}}
\newcommand{\bR}{\bm{R}}
\newcommand{\bS}{\bm{S}}
\newcommand{\bT}{\bm{T}}
\newcommand{\bU}{\bm{U}}
\newcommand{\bV}{\bm{V}}
\newcommand{\bW}{\bm{W}}
\newcommand{\bX}{\bm{X}}
\newcommand{\bY}{\bm{Y}}
\newcommand{\bZ}{\bm{Z}}
\newcommand{\ba}{\bm{a}}
\newcommand{\bb}{\bm{b}}
\newcommand{\bc}{\bm{c}}
\newcommand{\bd}{\bm{d}}
\newcommand{\be}{\bm{e}}
\newcommand{\bbf}{\bm{f}}
\newcommand{\bg}{\bm{g}}
\newcommand{\bh}{\bm{h}}
\newcommand{\bi}{\bmf{i}}
\newcommand{\bj}{\bm{j}}
\newcommand{\bk}{\bm{k}}
\newcommand{\bl}{\bm{l}}
\newcommand{\bbm}{\bm{m}}
\newcommand{\bn}{\bm{n}}
\newcommand{\bo}{\bm{o}}
\newcommand{\bp}{\bm{p}}
\newcommand{\bq}{\bm{q}}
\newcommand{\br}{\bm{r}}
\newcommand{\bs}{\bm{s}}
\newcommand{\bt}{\bm{t}}
\newcommand{\bu}{\bm{u}}
\newcommand{\bv}{\bm{v}}
\newcommand{\bw}{\bm{w}}
\newcommand{\bx}{\bm{x}}
\newcommand{\by}{\bm{y}}
\newcommand{\bz}{\bm{z}}
\newcommand{\EE}{\mathbb{E}}
\newcommand{\cL}{\mathcal{L}}
\begin{align}\label{eq:na-risk}
&\ell_{\rm NA}(\tilde{\bY}^{c}, f(\tilde{\bX}; \theta)) \notag\\ &=\EE_{\tilde{\bY}_m=\tilde{\bY}_m^{c}|\tilde{\bX}_m}
\cL(\tilde{\bY}_m^{c}, f(\tilde{\bX}_m; \theta) , \mathbb{1}(\tilde{\bY}_m=\tilde{\bY}_m^{c})) \notag\\
&=\hat{P}(\tilde{\bY}^{c}=\tilde{\bY}|\tilde{\bX}) \ell(\tilde{\bY}^{c}, f(\tilde{\bX}; \theta)) + \notag\\
&~~~~~\hat{P}(\tilde{\bY}^{c}\neq\tilde{\bY}|\tilde{\bX}) \ell^{-}(\tilde{\bY}^{c}, f(\tilde{\bX}; \theta)),
\end{align}
where \hat{P} is estimated using histogram binning on the dev set.
Comments
- This confidence aware loss function is well designed.
- I’m not fully convinced that CRF scores will still have such a strong correlation with the probability of labels being correct on out-of-domain data. But well, the author did what they can.
Rating
- 5: Transformative: This paper is likely to change our field. It should be considered for a best paper award.
- 4.5: Exciting: It changed my thinking on this topic. I would fight for it to be accepted.
- 4: Strong: I learned a lot from it. I would like to see it accepted.
- 3.5: Leaning positive: It can be accepted more or less in its current form. However, the work it describes is not particularly exciting and/or inspiring, so it will not be a big loss if people don’t see it in this conference.
- 3: Ambivalent: It has merits (e.g., it reports state-of-the-art results, the idea is nice), but there are key weaknesses (e.g., I didn’t learn much from it, evaluation is not convincing, it describes incremental work). I believe it can significantly benefit from another round of revision, but I won’t object to accepting it if my co-reviewers are willing to champion it.
- 2.5: Leaning negative: I am leaning towards rejection, but I can be persuaded if my co-reviewers think otherwise.
- 2: Mediocre: I would rather not see it in the conference.
- 1.5: Weak: I am pretty confident that it should be rejected.
- 1: Poor: I would fight to have it rejected.
0 投票者