Do Transformers Really Perform Bad for Graph Representation?

Machine Learning Graph Learning
#1

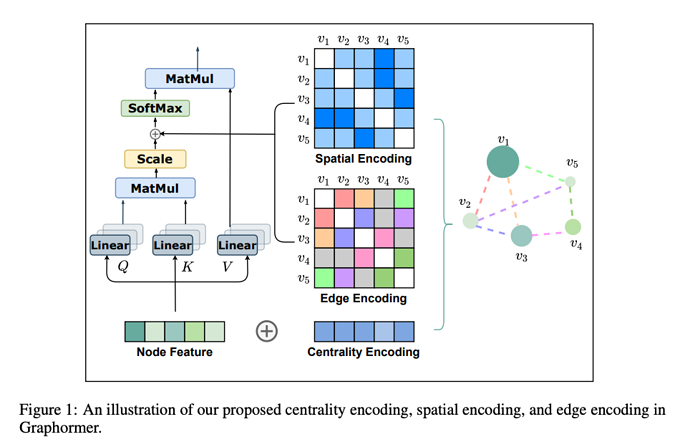
This paper presents an effective graph Transformer architecture for encoding structural information. Specifically, they propose 3 encoding methods to model graph structures.

1
1964×624 86.5 KB

  1. Centrality Encoding

    h_i^{(0)} = x_i + z^-_{\text{deg}^{-}(v_i)} + z^+_{\text{deg}^{+}(v_i)},

    where z^{-}, z^{+} \in \mathbb{R}^d are learnable embedding vectors specified by the indegree \text{deg}^{-}(v_i) and outdegree \text{deg}^{+}(v_i) respectively.

  2. Spatial Encoding

    A_{ij}=\frac{(h_iW_{Q})(h_jW_{K})^T}{\sqrt{d}} + b_{\phi(v_i,v_j)},

    where \phi(v_i,v_j) is the distance of the shortest path (SPD) between v_i and v_j, b_{\phi(v_i,v_j)} is a learnable scalar indexed by \phi(v_i,v_j), and shared across all layers.

  3. Edge Encoding in the Attention

A_{ij}=\frac{(h_iW_{Q})(h_jW_{K})^T}{\sqrt{d}} + b_{\phi(v_i,v_j)} + c_{ij},\ \text{where}\ c_{ij}=\frac{1}{N}\sum_{n=1}^{N} x_{e_n}(w^{E}_{n})^T,

where x_{e_n} is the feature of the n-th edge e_n in the shortest path \text{SP}_{ij}, w_n^{E}\in \mathbb{R}^{d_E} is the n-th weight embedding, and d_E is the dimensionality of edge feature.

Comments

  • Though the empirical results are good, most encoding methods affect only the attention map via SP, which means distance is all you need?
  • The average pooling of edges along SP is not intuitive as it completely ignores the order.
Rating
  • 5: Transformative: This paper is likely to change our field. It should be considered for a best paper award.
  • 4.5: Exciting: It changed my thinking on this topic. I would fight for it to be accepted.
  • 4: Strong: I learned a lot from it. I would like to see it accepted.
  • 3.5: Leaning positive: It can be accepted more or less in its current form. However, the work it describes is not particularly exciting and/or inspiring, so it will not be a big loss if people don’t see it in this conference.
  • 3: Ambivalent: It has merits (e.g., it reports state-of-the-art results, the idea is nice), but there are key weaknesses (e.g., I didn’t learn much from it, evaluation is not convincing, it describes incremental work). I believe it can significantly benefit from another round of revision, but I won’t object to accepting it if my co-reviewers are willing to champion it.
  • 2.5: Leaning negative: I am leaning towards rejection, but I can be persuaded if my co-reviewers think otherwise.
  • 2: Mediocre: I would rather not see it in the conference.
  • 1.5: Weak: I am pretty confident that it should be rejected.
  • 1: Poor: I would fight to have it rejected.

0 投票者