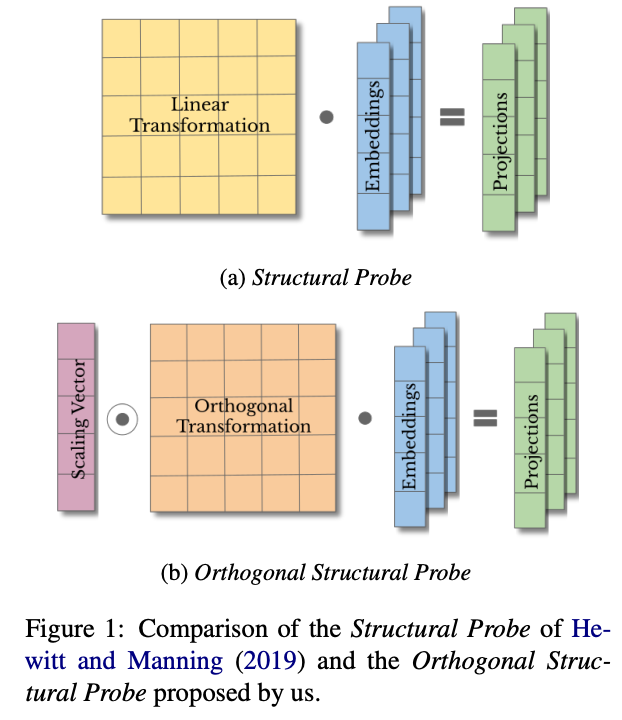
This paper introduces orthogonality to linear structural probes by SVD and use the diagonal D matrix as a weight vector for several MTL tasks. By coercing both orthogonality and sparsity, they are able to find embedding subspace capable of representing a particular linguistic structure.
Comments
- To be honest, I did not go over the mathematical derivation so my understanding might be wrong.
- Though layer-wise analyses are comprehensive, they are also well studied. I’m expecting a subspace analysis like which dimensions are used for tree depth and which are for tree distance, but I did not see such.
Rating
- 5: Transformative: This paper is likely to change our field. It should be considered for a best paper award.
- 4.5: Exciting: It changed my thinking on this topic. I would fight for it to be accepted.
- 4: Strong: I learned a lot from it. I would like to see it accepted.
- 3.5: Leaning positive: It can be accepted more or less in its current form. However, the work it describes is not particularly exciting and/or inspiring, so it will not be a big loss if people don’t see it in this conference.
- 3: Ambivalent: It has merits (e.g., it reports state-of-the-art results, the idea is nice), but there are key weaknesses (e.g., I didn’t learn much from it, evaluation is not convincing, it describes incremental work). I believe it can significantly benefit from another round of revision, but I won’t object to accepting it if my co-reviewers are willing to champion it.
- 2.5: Leaning negative: I am leaning towards rejection, but I can be persuaded if my co-reviewers think otherwise.
- 2: Mediocre: I would rather not see it in the conference.
- 1.5: Weak: I am pretty confident that it should be rejected.
- 1: Poor: I would fight to have it rejected.
0 投票者
